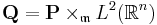Symplectic spinor bundle
In differential geometry, given a metaplectic structure 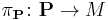 on a
on a 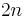 -dimensional symplectic manifold
-dimensional symplectic manifold 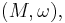 one defines the symplectic spinor bundle to be the Hilbert space bundle
one defines the symplectic spinor bundle to be the Hilbert space bundle 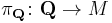 associated to the metaplectic structure via the metaplectic representation. The metaplectic representation of the metaplectic group —the two-fold covering of the symplectic group— gives rise to a infinite rank vector bundle, this is the symplectic spinor construction due to Bertram Kostant.[1]
associated to the metaplectic structure via the metaplectic representation. The metaplectic representation of the metaplectic group —the two-fold covering of the symplectic group— gives rise to a infinite rank vector bundle, this is the symplectic spinor construction due to Bertram Kostant.[1]
A section of the symplectic spinor bundle 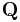 is called a symplectic spinor field.
is called a symplectic spinor field.
Contents |
Formal definition
Let 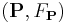 be a metaplectic structure on a symplectic manifold
be a metaplectic structure on a symplectic manifold  that is, an equivariant lift of the symplectic frame bundle
that is, an equivariant lift of the symplectic frame bundle 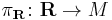 with respect to the double covering
with respect to the double covering 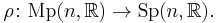
The symplectic spinor bundle 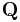 is defined [2] to be the Hilbert space bundle
is defined [2] to be the Hilbert space bundle
associated to the metaplectic structure 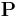 via the metaplectic representation
via the metaplectic representation 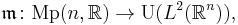 also called the Segal-Shale-Weil [3][4][5] representation of
also called the Segal-Shale-Weil [3][4][5] representation of 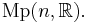 Here, the notation
Here, the notation 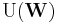 denotes the group of unitary operators acting on a Hilbert space
denotes the group of unitary operators acting on a Hilbert space 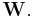
The Segal-Shale-Weil representation [6] is an infinite dimensional unitary representation of the metaplectic group 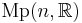 on the space of all complex valued square Lebesgue integrable functions
on the space of all complex valued square Lebesgue integrable functions 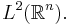 Because of the infinite dimension, the Segal-Shale-Weil representation is not so easy to handle.
Because of the infinite dimension, the Segal-Shale-Weil representation is not so easy to handle.
See also
Notes
- ^ Kostant, B. (1974). "Symplectic Spinors". Symposia Mathematica (Academic Press) XIV: 139–152.
- ^ Habermann, Katharina; Habermann, Lutz (2006), Introduction to Symplectic Dirac Operators, Springer-Verlag, ISBN 978-3-540-33420-0 page 37
- ^ Segal, I.E (1962), Lectures at the 1960 Boulder Summer Seminar, AMS, Providence, RI
- ^ Shale, D. (1962). "Linear symmetries of free boson fields". Trans. Amer. Math. Soc. 103: 149–167.
- ^ Weil, A. (1964). "Sur certains groupes d’opérateurs unitaires". Acta Math. 111: 143–211. doi:10.1007/BF02391012.
- ^ Kashiwara, M; Vergne, M. (1978). "On the Segal-Shale-Weil representation and harmonic polynomials". Inventiones Mathematicae 44: 1–47. doi:10.1007/BF01389900.
Books
- Habermann, Katharina; Habermann, Lutz (2006), Introduction to Symplectic Dirac Operators, Springer-Verlag, ISBN 978-3-540-33420-0